This example was automatically generated from a Jupyter notebook in the RxInferExamples.jl repository.
We welcome and encourage contributions! You can help by:
- Improving this example
- Creating new examples
- Reporting issues or bugs
- Suggesting enhancements
Visit our GitHub repository to get started. Together we can make RxInfer.jl even better! 💪
Recurrent Switching Linear Dynamical System
This is an experimental example of a Recurrent Switching Linear Dynamical System (RSLDS) model. The notebook requires patches to RxInfer and ReactiveMP, which are condensed in the hidden blocks below.
Hidden block of RxInfer & ReactiveMP patches and extensions - click to expand
using ExponentialFamily, RxInfer, BayesBase, GraphPPL
import ReactiveMP: AbstractFactorNode, NodeInterface, IndexedNodeInterface, FactorNodeActivationOptions, Marginalisation,
Deterministic, PredefinedNodeFunctionalForm,FunctionalDependencies, collect_functional_dependencies, activate!, functional_dependencies,
collect_latest_messages, collect_latest_marginals, marginalrule, rule, name, getinboundinterfaces, clustername, getdependecies,
messagein, ManyOf, getvariable
import ExponentialFamily: getnaturalparameters, exponential_family_typetag
export Gate, GateNode
# Mixture Functional Form
struct Gate{N} end
ReactiveMP.as_node_symbol(::Type{<:Gate}) = :Gate
ReactiveMP.interfaces(::Type{<:Gate}) = Val((:out, :switch, :inputs))
ReactiveMP.alias_interface(::Type{<:Gate}, ::Int64, name::Symbol) = name
ReactiveMP.is_predefined_node(::Type{<:Gate}) = ReactiveMP.PredefinedNodeFunctionalForm()
ReactiveMP.sdtype(::Type{<:Gate}) = ReactiveMP.Deterministic()
ReactiveMP.collect_factorisation(::Type{<:Gate}, factorization) = GateNodeFactorisation()
struct GateNodeFactorisation end
struct GateNode{N} <: ReactiveMP.AbstractFactorNode
out :: ReactiveMP.NodeInterface
switch :: ReactiveMP.NodeInterface
inputs :: NTuple{N, ReactiveMP.IndexedNodeInterface}
end
ReactiveMP.functionalform(factornode::GateNode{N}) where {N} = Gate{N}
ReactiveMP.getinterfaces(factornode::GateNode) = (factornode.out, factornode.switch, factornode.inputs...)
ReactiveMP.sdtype(factornode::GateNode) = ReactiveMP.Deterministic()
ReactiveMP.interfaceindices(factornode::GateNode, iname::Symbol) = (ReactiveMP.interfaceindex(factornode, iname),)
ReactiveMP.interfaceindices(factornode::GateNode, inames::NTuple{N, Symbol}) where {N} = map(iname -> ReactiveMP.interfaceindex(factornode, iname), inames)
ReactiveMP.interfaceindex(factornode::GateNode, iname::Symbol) = begin
if iname === :out
return 1
elseif iname === :switch
return 2
elseif iname === :inputs
return 3
end
end
ReactiveMP.factornode(::Type{<:Gate}, interfaces, factorization) = begin
outinterface = interfaces[findfirst(((name, variable),) -> name == :out, interfaces)]
switchinterface = interfaces[findfirst(((name, variable),) -> name == :switch, interfaces)]
inputinterfaces = filter(((name, variable),) -> name == :inputs, interfaces)
N = length(inputinterfaces)
return GateNode(ReactiveMP.NodeInterface(outinterface...), ReactiveMP.NodeInterface(switchinterface...), ntuple(i -> ReactiveMP.IndexedNodeInterface(i, ReactiveMP.NodeInterface(inputinterfaces[i]...)), N))
end
struct GateNodeInboundInterfaces end
ReactiveMP.getinboundinterfaces(::GateNode) = GateNodeInboundInterfaces()
ReactiveMP.clustername(::GateNodeInboundInterfaces) = :switch_inputs
struct GateNodeFunctionalDependencies <: FunctionalDependencies end
ReactiveMP.collect_functional_dependencies(::GateNode, ::Nothing) = GateNodeFunctionalDependencies()
ReactiveMP.collect_functional_dependencies(::GateNode, ::GateNodeFunctionalDependencies) = GateNodeFunctionalDependencies()
ReactiveMP.collect_functional_dependencies(::GateNode, ::Any) =
error("The functional dependencies for GateNode must be either `Nothing` or `GateNodeFunctionalDependencies`")
ReactiveMP.activate!(factornode::GateNode, options::FactorNodeActivationOptions) = begin
dependencies = ReactiveMP.collect_functional_dependencies(factornode, ReactiveMP.getdependecies(options))
return ReactiveMP.activate!(dependencies, factornode, options)
end
ReactiveMP.functional_dependencies(::GateNodeFunctionalDependencies, factornode::GateNode{N}, interface, iindex::Int) where {N} = begin
message_dependencies = if iindex === 1
# output depends on input messages:
(factornode.inputs, )
elseif iindex === 2
# switch depends on:
(factornode.out, factornode.inputs)
elseif 2 < iindex <= N + 2
# k'th input depends on:
(factornode.out, )
else
error("Bad index in functional_dependencies for MixtureNode")
end
marginal_dependencies = if iindex === 1
# output depends on:
(factornode.switch, )
elseif iindex === 2
# switch depends on:
( )
elseif 2 < iindex <= N + 2
# k'th input depends on:
(factornode.switch,)
else
error("Bad index in functional_dependencies for GateNode")
end
return message_dependencies, marginal_dependencies
end
ReactiveMP.collect_latest_messages(::GateNodeFunctionalDependencies, factornode::GateNode{N}, messages::Tuple{NodeInterface}) where {N} = begin
outputinterface = messages[1]
msgs_names = Val{(name(outputinterface),)}()
msgs_observable = combineLatestUpdates((messagein(outputinterface),), PushNew())
return msgs_names, msgs_observable
end
ReactiveMP.collect_latest_marginals(::GateNodeFunctionalDependencies, factornode::GateNode{N}, marginals::Tuple{NodeInterface}) where {N} = begin
switchinterface = marginals[1]
marginal_names = Val{(name(switchinterface),)}()
marginal_observable = combineLatestUpdates((
getmarginal(getvariable(switchinterface), IncludeAll()),
), PushNew())
return marginal_names, marginal_observable
end
ReactiveMP.collect_latest_marginals(::GateNodeFunctionalDependencies, factornode::GateNode{N}, marginals::NTuple{N,IndexedNodeInterface}) where {N} = begin
inputsinterfaces = marginals
marginal_names = Val{(name(first(inputsinterfaces)),)}()
marginal_observable = combineLatest(map(input -> getmarginal(getvariable(input), IncludeAll()), inputsinterfaces), PushNew()) |> map_to((ManyOf(map(input -> getmarginal(getvariable(input), IncludeAll()), inputsinterfaces)),))
return marginal_names, marginal_observable
end
ReactiveMP.collect_latest_messages(::GateNodeFunctionalDependencies, factornode::GateNode{N}, messages::Tuple{NodeInterface, NTuple{N, IndexedNodeInterface}}) where {N} = begin
output_or_switch_interface = messages[1]
inputsinterfaces = messages[2]
msgs_names = Val{(name(output_or_switch_interface), name(inputsinterfaces[1]))}()
msgs_observable =
combineLatest(
(messagein(output_or_switch_interface), combineLatest(map(input -> messagein(input), inputsinterfaces), PushNew())),
PushNew()
) |> map_to((
messagein(output_or_switch_interface),
ManyOf(map(input -> messagein(input), inputsinterfaces))
))
return msgs_names, msgs_observable
end
ReactiveMP.collect_latest_messages(::GateNodeFunctionalDependencies, factornode::GateNode{N}, messages::Tuple{NTuple{N,IndexedNodeInterface}}) where {N} = begin
inputsinterfaces = messages[1]
msgs_names = Val{(name(first(inputsinterfaces)),)}()
msgs_observable = combineLatest(map(input -> messagein(input), inputsinterfaces), PushNew()) |> map_to((ManyOf(map(input -> messagein(input), inputsinterfaces)),))
return msgs_names, msgs_observable
end
ReactiveMP.marginalrule(fform::Type{<:Gate}, on::Val{:switch_inputs}, mnames::Any, messages::Any, qnames::Nothing, marginals::Nothing, meta::Nothing, __node::Any) = begin
# m_out = getdata(messages[1])
m_switch = getdata(messages[2])
m_inputs = getdata.(messages[3:end])
return FactorizedJoint((m_inputs..., m_switch))
end
ReactiveMP.@rule Gate(:out, Marginalisation) (q_switch::Any, m_inputs::ManyOf{N, Any}) where {N} = begin
return MixtureDistribution(collect(m_inputs), probvec(q_switch))
end
ReactiveMP.@rule Gate(:switch, Marginalisation) (m_out::Any, m_inputs::ManyOf{N, Any}) where {N} = begin
logscales = map(input -> compute_logscale(prod(GenericProd(),m_out,input), m_out, input), m_inputs)
p = softmax(collect(logscales))
return Multinomial(1, p)
end
ReactiveMP.@rule Gate((:inputs, k), Marginalisation) (m_out::Any, q_switch::Any,) = begin
z = probvec(q_switch)[k]
ef_out = convert(ExponentialFamilyDistribution, m_out)
η = getnaturalparameters(ef_out)
ef_opt = ExponentialFamilyDistribution(exponential_family_typetag(ef_out), η * z)
return convert(Distribution, ef_opt)
end
ReactiveMP.@rule typeof(*)(:out, Marginalisation) (m_A::PointMass, m_in::MixtureDistribution, meta::Any) = begin
comps = BayesBase.components(m_in)
new_components = similar(comps)
@inbounds for (i,component) in enumerate(comps)
new_components[i] = @call_rule typeof(*)(:out, Marginalisation) (m_A = m_A, m_in = component, meta = meta)
end
dist = MixtureDistribution(new_components, BayesBase.weights(m_in))
return dist
end
ReactiveMP.@rule typeof(dot)(:out, Marginalisation) (m_in1::MixtureDistribution, m_in2::PointMass, meta::Any) = begin
comps = BayesBase.components(m_in1)
new_components = []
@inbounds for (i, component) in enumerate(comps)
push!(new_components, @call_rule typeof(dot)(:out, Marginalisation) (m_in1 = component, m_in2 = m_in2, meta = meta))
end
mixture = MixtureDistribution(new_components, BayesBase.weights(m_in1))
return mixture
end
@rule typeof(dot)(:in1, Marginalisation) (m_out::MixtureDistribution, m_in2::PointMass, meta::Any) = begin
comps = BayesBase.components(m_out)
weights = BayesBase.weights(m_out)
new_comps = []
for (comp, weight) in zip(comps, weights)
new_comp = @call_rule typeof(dot)(:in1, Marginalisation) (m_out = comp, m_in2 = m_in2, meta = meta)
push!(new_comps, new_comp)
end
return MixtureDistribution(new_comps, weights)
end
function BayesBase.prod(::BayesBase.UnspecifiedProd, left::GaussianDistributionsFamily, right::MixtureDistribution)
comps = BayesBase.components(right)
weights = BayesBase.weights(right)
new_comps = []
for comp in comps
new_comp = prod(GenericProd(),left, comp)
push!(new_comps, new_comp)
end
return MixtureDistribution(new_comps, weights)
end
BayesBase.prod(::BayesBase.UnspecifiedProd, left::MixtureDistribution, right::GaussianDistributionsFamily) = prod(GenericProd(),right, left)
BayesBase.paramfloattype(::MixtureDistribution) = Float64
import ExponentialFamily.LogExpFunctions: logsumexp
function BayesBase.prod(::GenericProd, left::Categorical, right::Multinomial)
@assert right.n == 1
right_cat = Categorical(right.p)
p = prod(GenericProd(), left, right_cat).p
return Multinomial(1, p)
end
BayesBase.prod(::GenericProd, left::Multinomial, right::Categorical) = prod(GenericProd(), right, left)
function BayesBase.prod(::GenericProd, left::Multinomial, right::Multinomial)
@assert left.n == right.n
p = left.p .* right.p
p = p ./ sum(p)
return Multinomial(left.n, p)
end
BayesBase.prod(::BayesBase.UnspecifiedProd, left::Multinomial, right::Multinomial) = prod(GenericProd(), left, right)
function BayesBase.compute_logscale(dist1::Multinomial, dist2::Multinomial, dist3::Multinomial)
logp1 = log.(dist1.p) - log(dist1.p[end])
logp2 = log.(dist2.p) - log(dist2.p[end])
logp3 = log.(dist3.p) - log(dist3.p[end])
return logsumexp(logp1) - logsumexp(logp2) - logsumexp(logp3)
end
BayesBase.compute_logscale(d1::ExponentialFamily.WishartFast, d2::ExponentialFamily.WishartFast, d3::ExponentialFamily.WishartFast) = begin
return logpartition(convert(ExponentialFamilyDistribution, d1)) - logpartition(convert(ExponentialFamilyDistribution, d2)) - logpartition(convert(ExponentialFamilyDistribution, d3))
end
ExponentialFamily.probvec(d::Multinomial) = d.p
@rule ContinuousTransition(:W, Marginalisation) (q_y_x::MultivariateNormalDistributionsFamily, q_a::MixtureDistribution, meta::Any) = begin
q_a_normal = convert(promote_variate_type(typeof(mean(q_a)), NormalMeanPrecision), mean(q_a), precision(q_a))
return @call_rule ContinuousTransition(:W, Marginalisation) (q_y_x = q_y_x, q_a = q_a_normal, meta = meta)
end
@rule ContinuousTransition(:y, Marginalisation) (m_x::MultivariateNormalDistributionsFamily, q_a::MixtureDistribution, q_W::Any, meta::Any) = begin
q_a_normal = convert(promote_variate_type(typeof(mean(q_a)), NormalMeanPrecision), mean(q_a), precision(q_a))
return @call_rule ContinuousTransition(:y, Marginalisation) (m_x = m_x, q_a = q_a_normal, q_W = q_W, meta = meta)
end
@rule ContinuousTransition(:a, Marginalisation) (q_y_x::MultivariateNormalDistributionsFamily, q_a::MixtureDistribution, q_W::Any, meta::Any) = begin
q_a_normal = convert(promote_variate_type(typeof(mean(q_a)), NormalMeanPrecision), mean(q_a), precision(q_a))
return @call_rule ContinuousTransition(:a, Marginalisation) (q_y_x = q_y_x, q_a = q_a_normal, q_W = q_W, meta = meta)
end
@rule ContinuousTransition(:x, Marginalisation) (m_y::MultivariateNormalDistributionsFamily , q_a::MixtureDistribution, q_W::Any, meta::Any) = begin
q_a_normal = convert(promote_variate_type(typeof(mean(q_a)), NormalMeanPrecision), mean(q_a), precision(q_a))
return @call_rule ContinuousTransition(:x, Marginalisation) (m_y = m_y, q_a = q_a_normal, q_W = q_W, meta = meta)
end
@rule ContinuousTransition(:y, Marginalisation) (m_x::MixtureDistribution, q_a::MultivariateNormalDistributionsFamily, q_W::Any, meta::Any) = begin
m_x_normal = convert(promote_variate_type(typeof(mean(m_x)), NormalMeanPrecision), mean(m_x), precision(m_x))
return @call_rule ContinuousTransition(:y, Marginalisation) (m_x = m_x_normal, q_a = q_a, q_W = q_W, meta = meta)
end
@marginalrule ContinuousTransition(:y_x) (m_y::MultivariateNormalDistributionsFamily, m_x::MixtureDistribution, q_a::MultivariateNormalDistributionsFamily, q_W::Any, meta::Any) = begin
m_x_normal = convert(promote_variate_type(typeof(mean(m_x)), NormalMeanPrecision), mean(m_x), precision(m_x))
return @call_marginalrule ContinuousTransition(:y_x) (m_y = m_y, m_x = m_x_normal, q_a = q_a, q_W = q_W, meta = meta)
end
@rule typeof(+)(:out, Marginalisation) (m_in1::MultivariateNormalDistributionsFamily, m_in2::MixtureDistribution, ) = begin
return @call_rule typeof(+)(:out, Marginalisation) (m_in1 = m_in1, m_in2 = convert(promote_variate_type(typeof(mean(m_in2)), NormalMeanPrecision), mean(m_in2), precision(m_in2)))
end
@rule typeof(+)(:in1, Marginalisation) (m_out::MultivariateNormalDistributionsFamily, m_in2::MixtureDistribution, ) = begin
return @call_rule typeof(+)(:in1, Marginalisation) (m_out = convert(promote_variate_type(typeof(mean(m_out)), NormalMeanPrecision), mean(m_out), precision(m_out)), m_in2 = convert(promote_variate_type(typeof(mean(m_in2)), NormalMeanPrecision), mean(m_in2), precision(m_in2)))
end
@rule DiscreteTransition(:out, Marginalisation) (m_in::Multinomial, q_a::DirichletCollection, ) = begin
@assert m_in.n == 1
p = probvec(m_in)
m_in_cat = Categorical(p)
return @call_rule DiscreteTransition(:out, Marginalisation) (m_in = m_in_cat, q_a = q_a)
end
@rule DiscreteTransition(:in, Marginalisation) (m_out::Multinomial, q_a::DirichletCollection, ) = begin
@assert m_out.n == 1
p = probvec(m_out)
m_out_cat = Categorical(p)
return @call_rule DiscreteTransition(:in, Marginalisation) (m_out = m_out_cat, q_a = q_a)
end
@marginalrule DiscreteTransition(:out_in) (m_out::Multinomial, m_in::Multinomial, q_a::DirichletCollection, ) = begin
@assert m_out.n == 1 && m_in.n == 1
p_out = probvec(m_out)
p_in = probvec(m_in)
m_out_cat = Categorical(p_out)
m_in_cat = Categorical(p_in)
return @call_marginalrule DiscreteTransition(:out_in) (m_out = m_out_cat, m_in = m_in_cat, q_a = q_a)
end
Base.length(d::MixtureDistribution) = length(d.components)
Base.ndims(d::MixtureDistribution) = first(size(first(d.components)))
ExponentialFamily.probvec(d::Multinomial) = d.p
BayesBase.entropy(d::MixtureDistribution) = mapreduce((c,w) -> w * BayesBase.entropy(c), +, d.components, d.weights)
BayesBase.mean(f::F, itr::MixtureDistribution) where {F} = mapreduce((c,w) -> w * mean(f, c), +, itr.components, itr.weights)
function create_P_matrix(n_switches)
P = zeros(n_switches, n_switches)
for i in 1:n_switches
P[i,:] = 0.5 * ones(n_switches)
P[i,i] = 1.0
end
return P
end
function BayesBase.mean(mixture::MixtureDistribution)
component_means = mean.(BayesBase.components(mixture))
component_weights = BayesBase.weights(mixture)
return mapreduce((m,w) -> w*m, +, component_means, component_weights)
end
function BayesBase.cov(mixture::MixtureDistribution)
component_cov = cov.(BayesBase.components(mixture))
component_means = mean.(BayesBase.components(mixture))
component_weights = BayesBase.weights(mixture)
mixture_mean = mean(mixture)
return mapreduce((v,m,w) -> w*(v + m*m'), +, component_cov, component_means, component_weights) - mixture_mean*mixture_mean'
end
BayesBase.precision(mixture::MixtureDistribution) = inv(cov(mixture))
function BayesBase.var(mixture::MixtureDistribution)
component_vars = var.(BayesBase.components(mixture))
component_means = mean.(BayesBase.components(mixture))
component_weights = BayesBase.weights(mixture)
mixture_mean = mean(mixture)
return mapreduce((v,m,w) -> w*(v + m.^2), +, component_vars, component_means, component_weights) - mixture_mean.^2
end
Hidden block of RSLDS Model Specification - click to expand
import ExponentialFamily: softmax
"""
RSLDSHyperparameters{T}
Structure containing hyperparameters for the Recurrent Switching Linear Dynamical System (RSLDS) model.
# Fields
- `a_w::T = 2.0`: Shape parameter for the Gamma prior on precision parameter w (when n_switches=1)
- `b_w::T = 2.0`: Rate parameter for the Gamma prior on precision parameter w (when n_switches=1)
- `Ψ_w::Matrix{T}`: Scale matrix for the Wishart prior on precision matrix w (when n_switches>1)
- `Ψ_R::Union{Matrix{T}, T}`: Scale matrix/parameter for the Wishart/Gamma prior on observation precision
- `ν_R::T`: Degrees of freedom for the Wishart prior on observation precision
- `α::Matrix{T}`: Parameter matrix for the Dirichlet prior on transition probabilities
- `C::Matrix{T}`: Observation matrix mapping latent states to observations
"""
Base.@kwdef struct RSLDSHyperparameters{T}
a_w::T = 2.0
b_w::T = 2.0
Ψ_w::Matrix{T}
Ψ_R::Union{Matrix{T}, T}
ν_R::T
α::Matrix{T}
C::Matrix{T}
end
"""
get_hyperparameters(hyperparameters::RSLDSHyperparameters)
Extract all hyperparameters from the RSLDSHyperparameters structure.
# Arguments
- `hyperparameters::RSLDSHyperparameters`: Structure containing the hyperparameters
# Returns
A tuple containing all hyperparameters in the order: a_w, b_w, Ψ_w, Ψ_R, ν_R, α, C
"""
function get_hyperparameters(hyperparameters::RSLDSHyperparameters)
return hyperparameters.a_w, hyperparameters.b_w, hyperparameters.Ψ_w, hyperparameters.Ψ_R, hyperparameters.ν_R, hyperparameters.α, hyperparameters.C
end
"""
default_hyperparameters(n_switches, obs_dim, dim_latent)
Create a default set of hyperparameters for the RSLDS model.
# Arguments
- `n_switches`: Number of switching states in the model
- `obs_dim`: Dimension of the observation space
- `dim_latent`: Dimension of the latent state space
# Returns
An RSLDSHyperparameters structure with default values
"""
function default_hyperparameters(n_switches, obs_dim, dim_latent)
return RSLDSHyperparameters(
a_w = 2.0,
b_w = 2.0,
Ψ_w = diageye(n_switches),
Ψ_R = diageye(obs_dim),
ν_R = obs_dim + 2.0,
α = ones(n_switches+1, n_switches+1),
C = diageye(obs_dim,dim_latent)
)
end
@model function rslds_model_learning(obs,n_obs,n_switches, dim_latent, η, Ψ, hyperparameters, learn_observation_covariance)
local H,A,Λ,u
transformation = (x) -> reshape(x, (dim_latent, dim_latent))
transformation2 = (x) -> reshape(x, (n_switches, dim_latent))
##Hyperparameters
a_w, b_w, Ψ_w, Ψ_R,ν_R, α, C = get_hyperparameters(hyperparameters)
## Priors on the parameters
if n_switches == 1
w ~ GammaShapeRate(a_w, b_w)
else
w ~ Wishart(n_switches+2,Ψ_w)
end
if learn_observation_covariance
if n_obs == 1
R ~ GammaShapeRate(ν_R, Ψ_R)
else
R ~ Wishart(ν_R, Ψ_R)
end
else
R = Ψ_R
end
for k in 1:n_switches+1
H[k] ~ MvNormalMeanCovariance(zeros(dim_latent^2), diageye(dim_latent^2))
Λ[k] ~ Wishart(dim_latent+2, diageye(dim_latent))
end
P ~ DirichletCollection(α)
ϕ ~ MvNormalMeanCovariance(zeros(dim_latent*n_switches), diageye(dim_latent*n_switches))
## States Initialisation
x[1] ~ MvNormalMeanCovariance(zeros(dim_latent), diageye(dim_latent))
for t in eachindex(obs)
## Recurrent Layer
if n_switches == 1
u[t] ~ softdot(ϕ, x[t], w)
else
u[t] ~ ContinuousTransition(x[t], ϕ, w) where {meta = CTMeta(transformation2)}
end
s[t] ~ MultinomialPolya(1, u[t]) where {dependencies = RequireMessageFunctionalDependencies(ψ = convert(promote_variate_type(typeof(η), NormalWeightedMeanPrecision), η, Ψ))}
s[t+1] ~ DiscreteTransition(s[t], P)
##Transition Layer
A[t] := Gate(switch=s[t+1], inputs=H)
B[t] := Gate(switch=s[t+1], inputs=Λ)
x[t+1] ~ ContinuousTransition(x[t], A[t], B[t]) where {meta = CTMeta(transformation)}
## Observation Layer
obs[t] ~ MvNormalMeanPrecision(C*x[t+1], R)
end
end
@constraints function rslds_learning_constraints(learn_observation_covariance)
if learn_observation_covariance
q(x,s,u,ϕ,w,P,H,A,Λ,B,R) = q(x,u)q(A)q(s)q(ϕ)q(w)q(P)q(H)q(Λ)q(B)q(R)
else
q(x,s,u,ϕ,w,P,H,A,Λ,B) = q(x,u)q(A)q(s)q(ϕ)q(w)q(P)q(H)q(Λ)q(B)
end
end
@initialization function rslds_learning_initmarginals(n_switches, dim_latent, obs_dim, learn_observation_covariance; rng = StableRNG(42))
q(x) = vague(MvNormalWeightedMeanPrecision, dim_latent)
q(s) = Multinomial(1,softmax(randn(rng, n_switches+1)))
q(ϕ) = vague(MvNormalWeightedMeanPrecision, dim_latent*(n_switches))
if n_switches == 1
q(w) = vague(GammaShapeRate)
else
q(w) = vague(Wishart, n_switches)
end
q(A) = vague(MvNormalWeightedMeanPrecision, dim_latent^2)
q(P) = DirichletCollection(ones(n_switches+1,n_switches+1))
q(Λ) = vague(Wishart, dim_latent)
q(H) = vague(MvNormalWeightedMeanPrecision, dim_latent^2)
q(B) = vague(Wishart, dim_latent)
if learn_observation_covariance
if obs_dim == 1
q(R) = vague(GammaShapeRate)
else
q(R) = Wishart(obs_dim+2, diageye(obs_dim))
end
end
end;
"""
fit_rslds(data, n_switches, dim_latent, n_obs; kwargs...)
Fit a Recurrent Switching Linear Dynamical System (RSLDS) model to the provided data.
# Arguments
- `data`: Time series observation data
- `n_switches`: Number of switching states in the model. Note: The user provides the total number of states,
but internally we use (n_switches-1) because the MultinomialPolya distribution adds an extra dimension
to represent the recurrent influence on state transitions.
- `dim_latent`: Dimension of the latent state space
- `n_obs`: Dimension of the observation space
# Keyword Arguments
- `iterations::Int = 60`: Number of inference iterations
- `η = nothing`: Mean parameter for the functional dependency in MultinomialPolya
- `Ψ = nothing`: Precision parameter for the functional dependency in MultinomialPolya
- `hyperparameters = nothing`: Custom hyperparameters for the model
- `progress::Bool = false`: Whether to show progress during inference
- `learn_observation_covariance::Bool = false`: Whether to learn the observation covariance
# Returns
The result of the inference procedure
"""
function fit_rslds(data, n_switches, dim_latent, n_obs; iterations = 60, η = nothing, Ψ = nothing, hyperparameters = nothing, progress = false, learn_observation_covariance = false)
@assert n_switches > 1 "n_switches must be greater than 1"
# We subtract 1 from n_switches because the MultinomialPolya distribution
# internally adds an extra dimension to represent the recurrent influence
# on state transitions. This convention allows the model to maintain the
# correct dimensionality while incorporating the recurrent dynamics.
n_switches = n_switches - 1
if hyperparameters === nothing
hyperparameters = default_hyperparameters(n_switches, length(data[1]), dim_latent)
end
if η === nothing
if n_switches == 1
η = 0.0
else
η = zeros(n_switches)
end
end
if Ψ === nothing
if n_switches == 1
Ψ = 0.0001
else
Ψ = 0.0001*diageye(n_switches)
end
end
model = rslds_model_learning(n_obs = n_obs, n_switches = n_switches, dim_latent = dim_latent, η = η, Ψ = Ψ, hyperparameters = hyperparameters, learn_observation_covariance = learn_observation_covariance)
constraints = rslds_learning_constraints(learn_observation_covariance)
initmarginals = rslds_learning_initmarginals(n_switches, dim_latent, n_obs, learn_observation_covariance)
return infer(model = model, data = (obs=data, ), constraints = constraints, initialization = initmarginals, iterations = iterations,
showprogress = progress,
returnvars = KeepEach(),
free_energy = true,
options = (limit_stack_depth = 100,)
)
end
#
function states_to_categorical(states)
return [argmax(states[t].p) for t in 1:length(states)]
end
Hidden block of Generating Synthetic Data - click to expand
using StableRNGs
function generate_switching_data(T, A1, A2, c, Q, R, x_0;rng = StableRNG(42))
# Initialize arrays to store states and observations
x = zeros(2, T) # State matrix: 2 dimensions × T timesteps
y = zeros(2, T) # Observation matrix: 2 dimensions × T timesteps
# Set initial state
x[:,1] = x_0
# Generate state transitions and observations
for t in 2:T
# Switch dynamics multiple times through the sequence
if t < T/3 || (t >= T/2 && t < 3T/4)
x[:,t] = A2 * x[:,t-1] + rand(rng,MvNormal(zeros(2), Q)) # First regime
else
x[:,t] = A1 * x[:,t-1] + rand(rng,MvNormal(zeros(2), Q)) # Second regime
end
# Generate observation from current state
y[:,t] = c * x[:,t] + rand(rng,MvNormal(zeros(2), R))
end
return x, y
end
# System parameters
T = 500 # Time horizon
θ = π / 15 # Rotation angle
# Define system matrices
A1 = [cos(θ) -sin(θ); sin(θ) cos(θ)] # Rotation matrix
A2 = [0.4 -0.01; 0.01 0.2]
c = [0.6 -0.02; -0.02 0.3] # Observation/distortion matrix
# Noise parameters
Q = [1.0 0.0; 0.0 1.0] # State noise covariance
R = [1.0 0.0; 0.0 1.0] # Observation noise variance
x_0 = [0.0, 0.0] # Initial state vector
# Generate synthetic data
x, y = generate_switching_data(T, A1, A2, c, Q, R, x_0)
y = [y[:,i] for i in 1:T]
x = [x[:,i] for i in 1:T]
hyperparameters = RSLDSHyperparameters(
a_w = 0.01,
b_w = 0.01,
Ψ_w = 10.0*diageye(2), # n-1
Ψ_R = inv(R),
ν_R = 4.0,
α = ones(2,2), # n
C = c
)Main.anonymous.RSLDSHyperparameters{Float64}(0.01, 0.01, [10.0 0.0; 0.0 10.
0], [1.0 0.0; 0.0 1.0], 4.0, [1.0 1.0; 1.0 1.0], [0.6 -0.02; -0.02 0.3])rslds_result = fit_rslds(y, 2, 2, 2; iterations = 150, hyperparameters = hyperparameters, progress = true)Inference results:
Posteriors | available for (ϕ, w, P, A, s, H, Λ, B, u, x)
Free Energy: | Real[386913.0, 75580.8, 2809.27, 2010.43, 1920.47, 186
5.65, 1893.55, 1933.31, 1972.41, 2010.39 … 1724.41, 1725.22, 1726.01, 172
6.79, 1727.56, 1728.32, 1729.06, 1729.79, 1730.51, 1731.22]using Plotsswitching_state_posterior = rslds_result.posteriors[:s][end];
states = states_to_categorical(switching_state_posterior);
scatter(states, label="Estimated Regimes", color="blue", linewidth=2)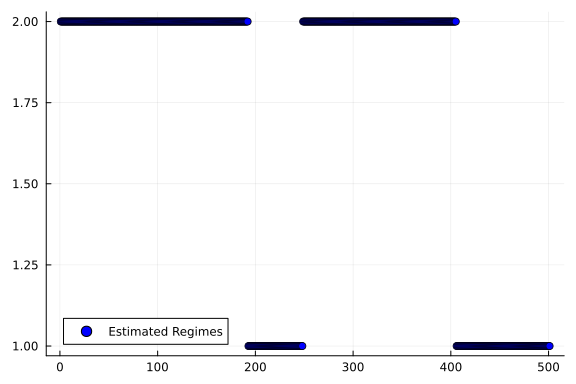
continuous_state_posterior = rslds_result.posteriors[:x][end];
index = 1
from = 1
to = 500
m_continuous = getindex.(mean.(continuous_state_posterior), index);
var_continuous = getindex.(var.(continuous_state_posterior), index);
plot(m_continuous[from+1:to], ribbon=sqrt.(var_continuous[from+1:to]), label="Estimated States", color="blue",fillalpha=0.2, linewidth=2)
plot!(getindex.(x,index)[from:to], label="True States", color="green", linewidth=1)
scatter!(getindex.(y,index)[from:to], label="Observed Data", color="black", ms=1.3)
lens!([10,50],[-3, 3],inset = (1, bbox(0.07, 0.6, 0.3, 0.3)), )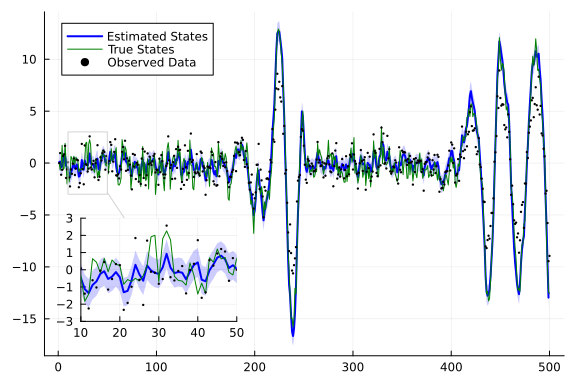
index = 2
m_continuous = getindex.(mean.(continuous_state_posterior), index);
var_continuous = getindex.(var.(continuous_state_posterior), index);
plot(m_continuous[from+1:to], ribbon=sqrt.(var_continuous[from+1:to]), label="Estimated States", color="blue",fillalpha=0.2, linewidth=2)
plot!(getindex.(x,index)[from:to], label="True States", color="green", linewidth=1)
scatter!(getindex.(y,index)[from:to], label="Observed Data", color="black", ms=1.3)
lens!([350,400],[-3, 3],inset = (1, bbox(0.07, 0.6, 0.3, 0.3)), )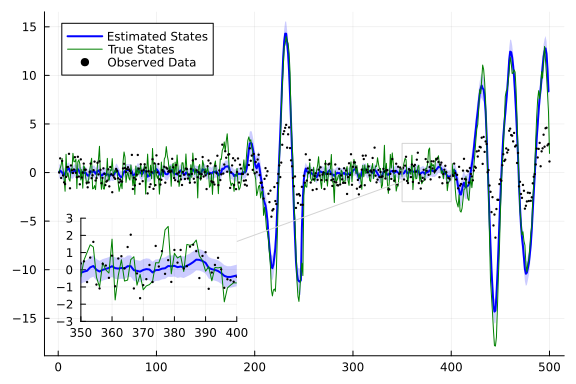
println("Estimated continuous transition matrices:")
println("----------------------------------------")
for i in 1:length(rslds_result.posteriors[:H][end])
println("Matrix $i:")
println(reshape(mean(rslds_result.posteriors[:H][end][i]), 2, 2))
println()
endEstimated continuous transition matrices:
----------------------------------------
Matrix 1:
[0.9801827287287435 -0.2096342513125255; 0.1905047312811018 0.9791493851524
091]
Matrix 2:
[0.5040325201488741 -0.3213042852544029; 0.10781013310895822 0.535126629567
7625]println("Estimated discrete transition matrix for HMM layer:")
println("----------------------------------------")
println(mean(rslds_result.posteriors[:P][end]))Estimated discrete transition matrix for HMM layer:
----------------------------------------
[0.9866080421546886 0.00863621309969759; 0.013391957845311477 0.99136378690
03024]This example was automatically generated from a Jupyter notebook in the RxInferExamples.jl repository.
We welcome and encourage contributions! You can help by:
- Improving this example
- Creating new examples
- Reporting issues or bugs
- Suggesting enhancements
Visit our GitHub repository to get started. Together we can make RxInfer.jl even better! 💪
This example was executed in a clean, isolated environment. Below are the exact package versions used:
For reproducibility:
- Use the same package versions when running locally
- Report any issues with package compatibility
Status `~/work/RxInferExamples.jl/RxInferExamples.jl/docs/src/categories/experimental_examples/recurrent_switching_linear_dynamical_system/Project.toml`
[b4ee3484] BayesBase v1.5.4
[62312e5e] ExponentialFamily v2.0.5
[b3f8163a] GraphPPL v4.6.2
[91a5bcdd] Plots v1.40.14
[a194aa59] ReactiveMP v5.5.0
[86711068] RxInfer v4.5.0
[860ef19b] StableRNGs v1.0.3